Project: "Theory and application of acoustic multipole radiators with complex singularities"
The aim of this project is to study and to clarify the mathematical and physical properties of complex multipole radiators. The source distributions that appear on the right side of the wave equation and produce single complex multipole radiators will be determined and the characteristic properties of the associated sound fields depending on the multipole order and position of the singularity in the complex plane will be investigated.
As starting point, we consider the monopole with its source position defined by real coordinates y=(y1,y2,y3) in three-dimensional space. The sound pressure is given by
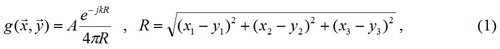
where A is the complex amplitude, x=(x1,x2,x3) the receiver position and k=w/c the wave number with the circular frequency w and the sound speed c.
The source position is then extended into the complex plane by adding an imaginary part
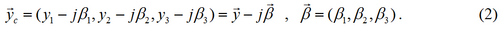
A complex monopole is the source whose position is given by (2) and generates a sound field written as
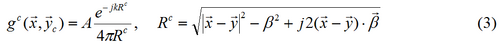
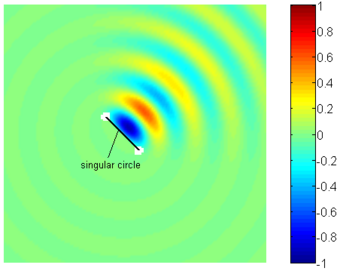
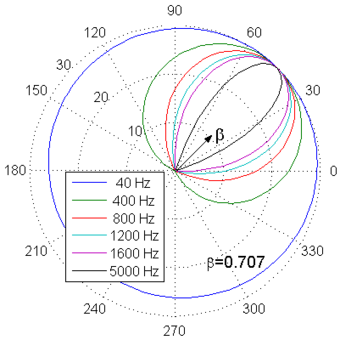
The sound of a complex monopole is radiated mainly in a half space and concentrated in the paraxial region near the axis given by β, for kβ>1, contrary to the uniformly radiation in the whole space of the usual monopole. The singularity of this type of source does not lie on one point but on a circle of radius β, centered on the point y, that lie on the plane perpendicular to β.
A possibility to generate general complex multipoles of higher order consists in differentiating gc with respect to the coordinates. Hence, a multipole of the order (n,m,l) is defined as:
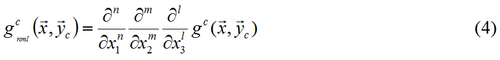
For illustration, a dipole of order (1,0,0) with imaginary part β=(6,0,0) and a lateral quadrupole of order(1,1,0) with imaginary part β=(0,0,3) were generated. The radiation pattern of both sources are shown in Fig. 3
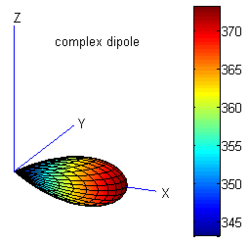
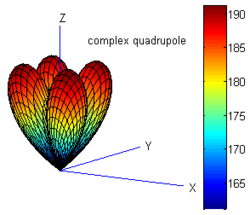
References
[1] M. Ochmann, The complex equivalent source method for sound propagation over an impedance
plane, J. Acoust. Soc. Am. 116 (6), 3304-3311, 2004.
[2] M. Ochmann, R. Piscoya, Erweiterung der Quellsimualtionstechnik auf Punktquellen mit komplexen
Quellorten, Fortschritte der Akustik, DAGA 2006, Braunschweig, 2006.
[3] M. Ochmann, R. Piscoya, The source simulation technique with complex source points for computing
acoustic radiation problems, Proceedings of the 13th International Congress on Sound and
Vibration (ICSV13), Wien, Austria, 2006.
[4] M. Ochmann, R. Piscoya, Acoustic multipoles with complex source points, 16th International
Congress on Sound and Vibration (ICSV16), July 2009, Krakow, Poland, 2009.
[5] M. Ochmann, Exact solutions for sound radiation from a moving monopole above an impedance
plane, J. Acoust. Soc. Am. 133 (4), 1911-1921, 2013.
